bài 47 trang 93 sgk toán 8 tập 1

Video chỉ dẫn giải

Bạn đang xem: bài 47 trang 93 sgk toán 8 tập 1

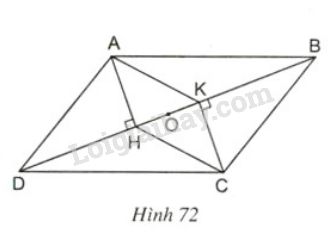
Cho hình \(72\), vô bại liệt \(ABCD\) là hình bình hành.

LG a.

Chứng minh rằng \(AHCK\) là hình bình hành.

Phương pháp giải:

Áp dụng: Dấu hiệu nhận ra hình bình hành: Tứ giác đem nhị cạnh đối tuy nhiên song và đều bằng nhau là hình bình hành.

Lời giải chi tiết:

Xét nhị tam giác vuông \(AHD\) và \(CKB\) có:

    +) \( AD = CB\) (vì \(ABCD\) là hình bình hành)

    +) \(\widehat {ADH} = \widehat {CBK}\) (hai góc ở địa điểm so sánh le vô, \(AD//BC\))

\( \Rightarrow \) \(∆AHD =  ∆CKB\) (cạnh huyền- góc nhọn)

\( \Rightarrow \) \(AH = CK\) (\(2\) cạnh tương ứng)

Xem thêm: yomost tiếng việt la gì

Ta có:

\(\left\{ \begin{array}{l}
AH \bot B{\rm{D}}\\
CK \bot B{\rm{D}}
\end{array} \right.\left( \text{giả thiết} \right) \Rightarrow AH//CK\)

Xét tứ giác \(AHCK\) có:

\(\left\{ \begin{array}{l}
AH//CK\\
AH = CK
\end{array} \right.\left( \text{chứng minh trên} \right)\)

\( \Rightarrow \) tứ giác \(AHCK\) là hình bình hành (dấu hiệu nhận ra hình bình hành).

Câu 2

Gọi \(O\) là trung điểm của \(HK\). Chứng minh rằng tía điểm \(A, O, C\) trực tiếp hàng

Phương pháp giải:

Áp dụng: Tính chất hình bình hành: Hai lối chéo cánh tách nhau bên trên trung điểm của từng lối.

Lời giải chi tiết:

Xét hình bình hành \(AHCK\) đem \(O\) là trung điểm của \(HK\) (giả thiết)

Xem thêm: nàng ngốc và quân sư

\( \Rightarrow \) \(O\) là giao phó điểm của hai tuyến phố chéo cánh \(AC\) và \(HK\) của hình bình hành (tính hóa học hình bình hành)

Hay \(A,O,C\) trực tiếp sản phẩm.

Loigiaihay.com